Analysis of Covariance

Analysis of Covariance is most important in statistics. To create models, we use Regression analysis which describes the effect of variation in predictor variables on the response variable. In some cases, if you have a categorical variable with values like Male/Female or Yes/No etc. Simple regression analysis gives several results for each value of the categorical variable. In this case, we need to search for this, this analysis is called Analysis of Covariance also called ANCOVA.

If we make a data frame in which a column represents the categorical variables like 0 or 1. Then it the data frame will depend on this column. Then we can check the effect of the categorical column on others. We used aov() function followed by anova() to compare multiple regressions.

Input Data

df <- data.frame (
  a = c(34, 67, 87,64,32,54,64,32,76, 56, 34,57,85,25, 78,65,54,43,65,55,43),
  b = c(6, 5, 8,5,4,4,5,5,3, 6, 5,4,5,8, 8,5,4,4,5,5,3),
  c = c(1,1,0,0,0,0,1,0,1,1,0,1,0,0,0,1,1,1,0,0,1)
)
print(head(df))

Output:

an1

Analysis of Covariance

Now we will create a regression model taking “b” as the predictor variable and “a” as the response variable taking into account the interaction between “c” and “b”.

A model with interaction between a categorical variable and predictor variable

df <- data.frame (
  a = c(34, 67, 87,64,32,54,64,32,76, 56, 34,57,85,25, 78,65,54,43,65,55,43),
  b = c(6, 5, 8,5,4,4,5,5,3, 6, 5,4,5,8, 8,5,4,4,5,5,3),
  c = c(1,1,0,0,0,0,1,0,1,1,0,1,0,0,0,1,1,1,0,0,1)
)

r <- aov(a~b*c,data = df)
print(summary(r))

Output:

an2

Model without interaction between a categorical variable and predictor variable

df <- data.frame (
  a = c(34, 67, 87,64,32,54,64,32,76, 56, 34,57,85,25, 78,65,54,43,65,55,43),
  b = c(6, 5, 8,5,4,4,5,5,3, 6, 5,4,5,8, 8,5,4,4,5,5,3),
  c = c(1,1,0,0,0,0,1,0,1,1,0,1,0,0,0,1,1,1,0,0,1)
)

r <- aov(a~b+c,data = df)
print(summary(r))

Output:

an3

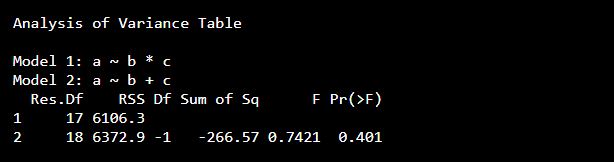
Comparing Two Models

Now we will use the anova() function to compare the two models to conclude if the interaction of the variables is truly insignificant.

df <- data.frame (
  a = c(34, 67, 87,64,32,54,64,32,76, 56, 34,57,85,25, 78,65,54,43,65,55,43),
  b = c(6, 5, 8,5,4,4,5,5,3, 6, 5,4,5,8, 8,5,4,4,5,5,3),
  c = c(1,1,0,0,0,0,1,0,1,1,0,1,0,0,0,1,1,1,0,0,1)
)
r1 <- aov(a~b*c,data = df)
r2 <- aov(a~b+c,data = df)

print(anova(r1,r2))

Output:

Analysis of Covariance