Matrix in R

The rectangular dataset in two dimensions is called a matrix in R programming. A matrix is created with a vector input to the matrix function. Mathematical operations can be performed like add, subtract, multiply, and division on a matrix in R programming.

Elements are arranged in a fixed number of rows and columns in the matrix. The matrix elements are the real numbers. We used matrix functions in R programming that can easily reproduce matrix memory representation. All the elements must share a common basic type in the matrix in R.

How to create a matrix in R?

R programming provides a function that creates a matrix-like vector and list. Matrix() function is used to create a matrix in R programming which played an important role in data analysis.

Have a look at the following syntax of the matrix:

The following terms are used in the syntax of the matrix in R:

data

In matrix function first argument is data. It is the input vector which is the data elements of the matrix.

nrow

The number of rows needs to create in the matrix is the second argument.

ncol

The number of columns needs to create in the matrix is the third argument

byrow

It is a logical clue. The input vector elements are arranged by row, in case its value is true.

dim_name

The name assigned to the rows and columns is known as dim_name parameter.

Following is an example to create a matrix and arranged the elements:

# Create a matrix
m <- matrix(c(1,2,3,4,5,6), nrow = 3, ncol = 2)

# Print the matrix
m

Output

1 18

Note: The c() function is used for items concatenation.

We can also create a string matrix:

m <- matrix(c("Python", "R", "Java", "C++", "Ruby", "HTML"), nrow = 2, ncol = 3)

m

Output

1 19

Accessing elements of matrix in R

We can easily access the elements of our matrix using the index of the element like C and C++. There are three different methods to access the elements from the matrix.

  1. Nth and mth column element can be accessed
  2. The elements present on the nth row can be accessed
  3. All the elements presented on the mth column can be accessed

Have a look at example to understand how elements are accessed from the matrix present on the nth row mth column, nth row, or mth column.

row_names = c("row1", "row2", "row3", "row4")  
col_names = c("col1", "col2", "col3")  

R <- matrix(c(5:16), nrow = 4, byrow = TRUE, dimnames = list(row_names, col_names))  
print(R)  
  
#Accessing element present on 3rd row and 2nd column  
print(R[3,2])  
  
#Accessing element present in 3rd row  
print(R[3,])  
  
#Accessing element present in 2nd column  
print(R[,2])

Output

1 20

Add Rows and Columns

To add additional columns in a Matrix we used the cbind() function: 

m <- matrix(c("Python", "R", "Java", "C++", "Ruby", "HTML"), nrow = 3, ncol = 2)

nm <- cbind(m, c("C#", "Basic", "JavaScript"))

# Print the new matrix
nm

Output

1 21

Remember: The cells length of the new column and existing column must be the same.

To add additional rows in a Matrix we used the rbind() function:

m <- matrix(c("Python", "R", "Java", "C++", "Ruby", "HTML"), nrow = 2, ncol = 3)
​
nm <- rbind(m, c("C#", "Basic", "JavaScript"))
​
# Print the new matrix
nm

Output

1 22

Remember: The cells length of new rows and existing rows must be the same.

Remove Rows and Columns

To remove rows and columns in a Matrix we used the c() function:

m <- matrix(c("Python", "R", "Java", "C++", "Ruby", "HTML"), nrow = 3, ncol =2)

#Remove the first row and the first column
m <- m[-c(1), -c(1)]

m

Output

1 23

Check if an Item Exists

To find out if a specified item is present in a matrix, use the %in% operator: The following example Check if “Java” is present in the matrix:

m <- matrix(c("Python", "R", "Java", "C++", "Ruby", "HTML"), nrow = 3, ncol = 2)

"Java" %in% m

Output

1 24

Amount of Rows and Columns

To find the number of rows and columns in a Matrix we used the dim() function:

m <- matrix(c("Python", "R", "Java", "C++", "Ruby", "HTML"), nrow = 3, ncol = 2)

dim(m)

Output

1 25

Matrix Length

To find the dimension of a Matrix we used the length() function:

m <- matrix(c("Python", "R", "Java", "C++", "Ruby", "HTML"), nrow = 3, ncol = 2)

length(m)

Output

1 26

In the example above: Dimension = 3*2 = 6.

Loop Through a Matrix

You can loop through a Matrix using a for loop. The loop will start at the first row, moving right:

m <- matrix(c("Python", "R", "Java", "C++", "Ruby", "HTML"), nrow = 3, ncol = 2)

for (rows in 1:nrow(m)) {
  for (columns in 1:ncol(m)) {
    print(m[rows, columns])
  }
}

Output

1 27

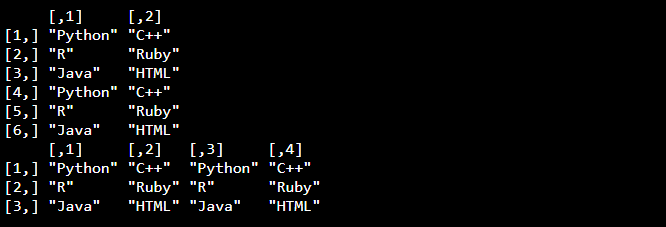
Combine two Matrices

We can use the rbind() or cbind() function again to combine two or more matrices together:

# Combine matrices
m1 <- matrix(c("Python", "R", "Java", "C++", "Ruby", "HTML"), nrow = 3, ncol = 2)
m2 <- matrix(c("Python", "R", "Java", "C++", "Ruby", "HTML"), nrow = 3, ncol = 2)

# Adding it as a rows
mc <- rbind(m1, m2)
mc

# Adding it as a columns
mc <- cbind(m1, m2)
mc

Output

1 28

Matrix operations

Mathematical operations can be performed on a matrix such as add, subtract, multiply in R programming. For mathematical action on the matrix, it is required that both the matrix should have equal dimensions.

Operations on Matrix in R
Operations on Matrix in R

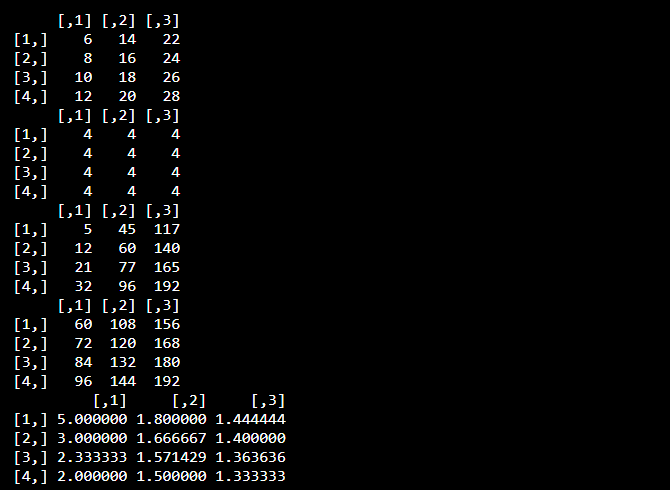
Look at the following example to check how mathematical operations are performed on the matrix.

R <- matrix(c(5:16), nrow = 4,ncol=3)  
S <- matrix(c(1:12), nrow = 4,ncol=3)  
  
#Addition  
sum<-R+S  
print(sum)  
  
#Subtraction  
sub<-R-S  
print(sub)  
  
#Multiplication  
mul<-R*S  
print(mul)  
  
#Multiplication by constant  
mul1<-R*12  
print(mul1)  
  
#Division  
div<-R/S  
print(div)

Output

1 29