As per statistics, the T-test in R is used to determine whether the mean of the two groups is equal to each other. The assumption for the test is that both groups are sampled from a normal distribution with equal fluctuation. There are two hypotheses used:
Null hypothesis:
It is assumed that the two means are the same.
Alternate hypothesis:
It is assumed that the two means are not the same.
There are two types of t-test in R
- One sample t-test
- Welch t-test
The t.test() function is used to provides a variety of t-test in R.
How to perform T-test in R
In the T-test, for specifying equal variances and a pooled variance estimate, we set var.equal=True. We can also use alternative=”less” or alternative=”greater” for specifying one-tailed test.
One-Sample T-test
One sample t-test is used to compares the mean of a vector against a theoretical mean. For t-test evaluation, we compute the p-value. The p-value ranges from 0 to 1. It is interpreted as:
- If the p-value is less than 0.05, it means we reject the null hypothesis.
- If the p-value is higher than 0.05, then it indicates that there is no evidance to reject the null hypothesis.
The syntax for performing one-sample t-test in R is as follow:
Here,
- x is the variable
- ? is described by the null hypothesis
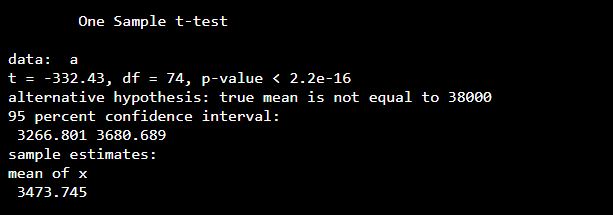
set.seed(0) a <- c(rnorm(75, mean = 3500, sd = 1000)) t.test(a, mu = 38000)
Output:
Paired-Sample T-test
We need two vectors data to perform a paired-sample test The syntax for paired sample test is as follow:
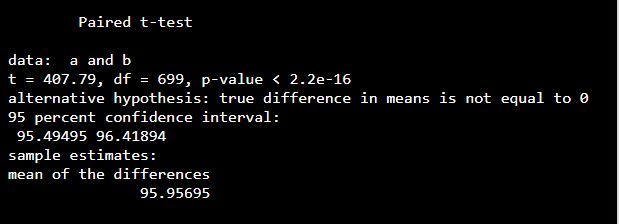
set.seed(1500) a <- c(rnorm(700, mean = 450, sd = 5)) b <- c(rnorm(700, mean = 354, sd = 4)) t.test(a, b, paired = TRUE)
Output:
Independent-Sample T-test
The independent-sample T-test can be taken in one of the three forms but it depends on the data structure and variance. These three forms are as follows:
- Independent-Samples T-test where v1 and v2 are numeric.
- Independent-Samples T-test where v1 is numeric and v2 is binary.
- Independent-Samples T-test with equal variances not assumed.
The syntax to perform an independent-sample t-test is as follow:
In R it is assumed that v1 and v2 are not equal, thus defaulting to Welch’s test. We set the flag var.equal=TRUE for toggling this.
Example 1: Independent-Sample T-test where y1 and y2 are numeric
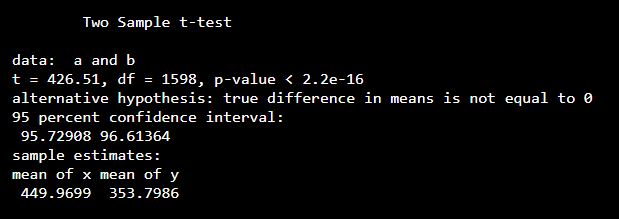
set.seed(0) a <- c(rnorm(800, mean = 450, sd = 5)) b <- c(rnorm(800, mean = 354, sd = 4)) t.test(a, b, var.equal = TRUE)
Output:
Example 2: Where y1 is numeric and y2 are binary
set.seed(0)
a <- c(rnorm(800, mean = 450, sd = 5))
b <- c(rnorm(800, mean = 354, sd = 4))
c <- c(a, b)
d <- c(rep("A", 800), rep("B", 800))
t.test(c ~ d, var.equal = TRUE)
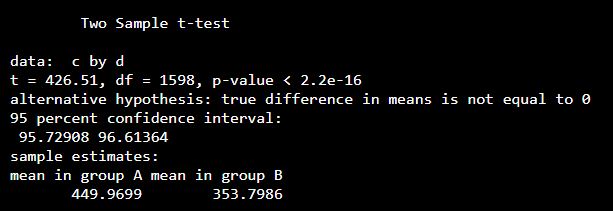
Example 3: With equal variance not assumed
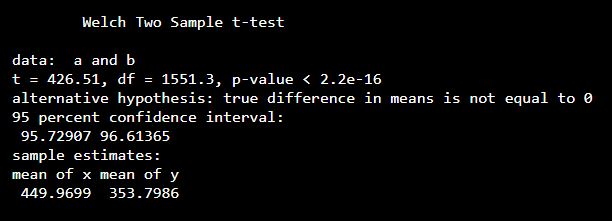
set.seed(0) a <- c(rnorm(800, mean = 450, sd = 5)) b <- c(rnorm(800, mean = 354, sd = 4)) t.test(a, b, var.equal = FALSE)
Output: